最近疫情被锁在家里半个月多月,有点无聊总想搞点什么,就突然想到我模拟这块在 niagara 上已经做过了基于欧拉视角的 NS 公式和 SPH 模拟流体,还有基于 PBD 的 rigid body dynamics,用 jocobi 迭代隐式积分求解 Mass-spring systems,都是基于 GPU 的效果,无奈 niagara 是个方便的 compute shader,就想着还有什么效果没做过的,就想到个 softbody,前面流体的 niagara 文章在知乎很多大佬都写过,在 b 站也有解析教程,但反观 rigidbody 和 softbody 的 niagara 文章比较少,相信有很多对模拟感兴趣同时又想在 niagara 实现的小伙伴在找文章方面上会走了很多弯路,加上 ue5 正式版已经发布了,所以就打算写一遍蹭一下热度(笑)
Softbody Dynamic 的模拟方法有很多,例如 FEM,Mass-spring systems,还有 shape matching。由于 shape mathcing 的方式做起来比较简单,也很合适并行。
那么先说一下本文做法的步骤。
- 首先在 houdini 用撒点把模型变为 1024 或者 512 甚至更少,只要是 2 的幂次方就行,因为是给 gpu 并行处理。然后记录每个顶点周围 4 个撒点 index 信息记录下来
- 做好 constraint,constraint 链接方式是每个点向法线 *-1 就是说向模型内部搜索一个锥型范围,得到点的序号存到一张 HDR 图里了,x 为点的总数,y 为当前点的 constraint。还要把这 512 点的 position 存成 512x1 的图,
- 在 niagara 采样 position 图生成点,然后在 simulate state 用 GetIndexByID 把当前点的 index 写入 grid2d,因为并行时候 index 是会随时变的,但 id 是唯一的,所以我们要记住这个粒子的 index
- 做 sdf collision
- 根据公式算出当前要匹配形状的点
- 对当前的点与要匹配的点做 lerp
- 输出这些点的信息,在材质进行 wpo
说完简易的步骤了,接下来说说详细的做法
首先在 houdini 里
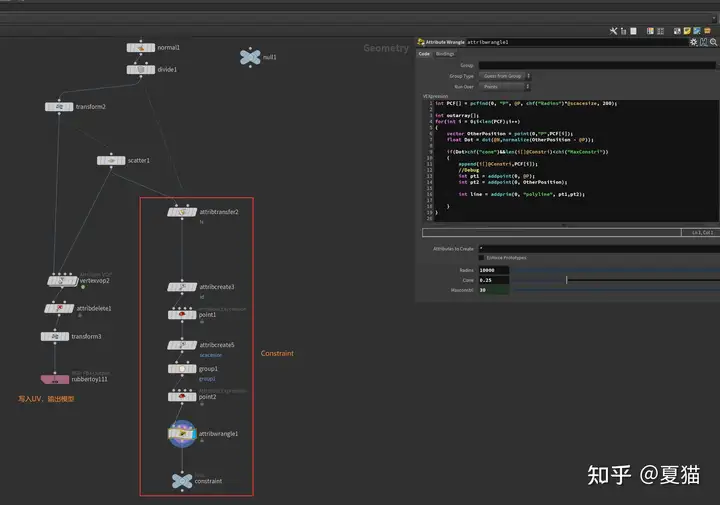
先建立 constraint,用 point cloud find 找到搜索周围的一圈点,用找到的点减自身对法线做个 dot,小于某个值的不要,此时有人会问我,这不是 pcopen 吗,pcopen 就已经有这些功能。其实是因为我太懒了,不想研究 pcopen 这函数 handle 怎么用,直接返回一组数我自己找到想要的数据,然后烘培图片,这里做 constraint 的时候要做多少个,可以自己定义,越多越硬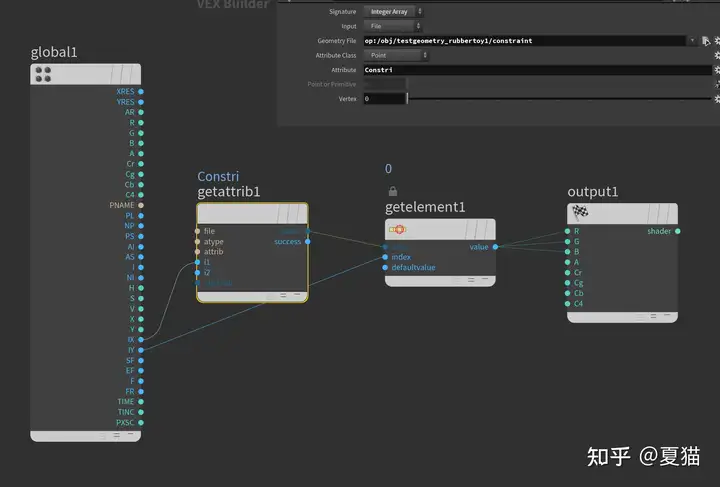

最后输出的图一定要为 exr,jpg 和 png 会把图片数据限制到 0~1
接下来就详细说说 shape matching 算法
这个算法已经有很多文章写的非常详细,包括 games103 中也有说过,所以现在按照我的理解再说一下 Shape Matching。
首先 Shape Matching 的思路是把一个刚体不当成一个刚体来看,把每个顶点当成自由的 particle,对每个点做单独的碰撞处理,然后再把这些点和他们的约束求 MSE(均方误差)恢复到物体原有的形状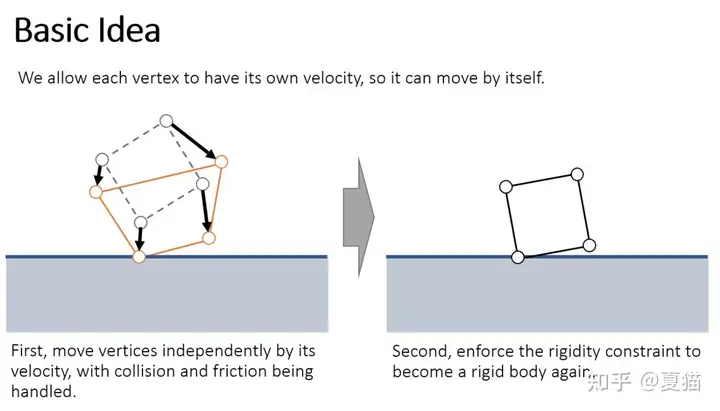
在当前帧,我们要 MSE 的表达式比较简单,直接求导数是极值点
其中 yi 是当前点的位置,c 是当前点的位置与他约束 (constrain) 的质心,R 是旋转矩阵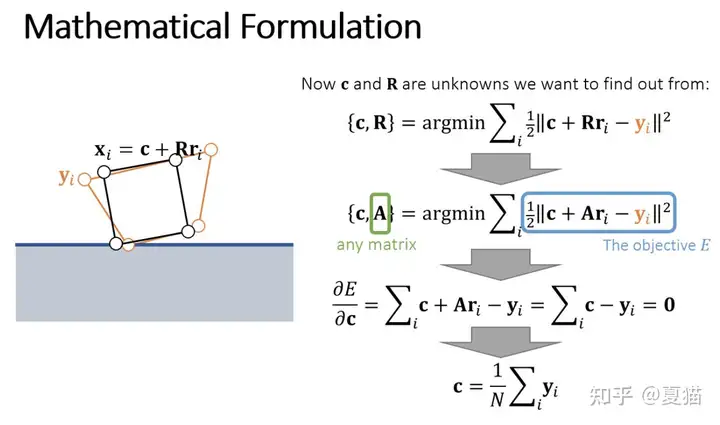
整理了以后很容易直观理解,就是对每个点和约束求位置的平均值,再对矩阵求导可得 A 矩阵,最后我们希望他是恢复到原来的形状,那么我们还要从 A 矩阵中提取旋转矩阵。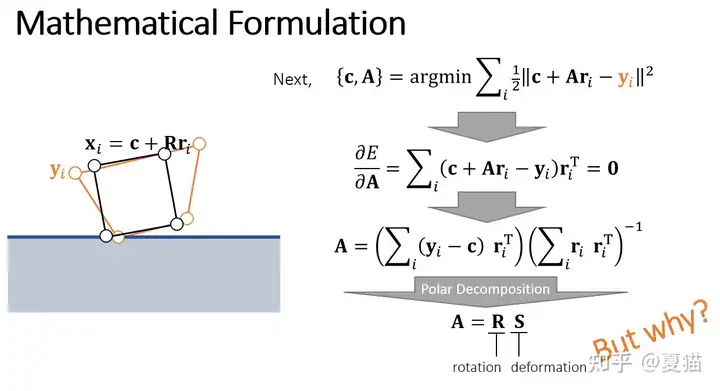
最简单的方法之一是使用极分解,通过对 A 的分解得到了旋转和形变矩阵,在 games103 中有见解,但今天要说的方法是另一种
这种方法是源自这篇 paper
https://matthias-research.github.io/pages/publications/stablePolarDecomp.pdf
这次说的新方法简单而有效,我们假设我们已经从模拟的上一个时间步或迭代求解的上一步得到一个近似值,而不是直接求解 R。
其中 exp (ω) 是轴为 ω/|ω| 的旋转矩阵和角度 |ω|,也称为指数映射 (exponential map),指数映射可以保证这个矩阵是合适的,既 ω= 0 的情况下行列式也等于 1,也就说明这个旋转矩阵不会改变物体体积的大小。在这种情况下它假设相同。因此,如果 R 是适当的旋转矩阵,则物体通过 update 保持不变。
那么我们要怎么选择这个 ω 的方向呢,最好的选择是用 Frobenius 范数,因为 F 范数可以让这个映射矩阵于原始矩阵的差尽可能小,为了找到这个方向,我们以物理方式来解释,让 a1,a2,a3 为 A 的列向量,r1,r2,r3 为 R 矩阵的列向量,R 矩阵只允许围绕着原点旋转。由于我们想最小化 F 我们定义的能量
我们将选择 ω 作为刚体在力 EF 下加速的轴。 作用在 R 轴尖端的力为
由于这些力作用在 R 上的总扭矩为
因此,我们为某个标量 α 而选择 ω = ατ。 τ 的引入允许对最小化 Frobenius 范数的矩阵 R 和通过对 矩阵 A 进行极分解获得的矩阵 R 进行新的解释。在 paper 附录中可以证明两者 τ = 0。
那么我们怎么选择这个标量 α,首先我们来看 ai 和 ri,如果我们选择 那么,就是两个向量的角度,然而我们的目标是对齐 ai 和 ri 让他们 τ = 0,如果 |ω| = φ 就是完成对齐了,
所以从 得到 所以最终我们产生了迭代公式
其中 是个安全参数,这方法与大多数现有方法相比,它可以粗暴地处理秩亏矩阵 A。在这种情况下,它会继承先前旋转矩阵 R 中的缺失信息。如果 ai 为零,则相应的扭矩分量也为零,并且 R 沿该方向的方向不变。在 A = 0 的极端情况下,总扭矩为零,R 保持不变。如果 a1 是唯一的非零轴,我们的方法会在 r1 和 a1 生成的平面中正确旋转 R 以将 ri 与 a1 对齐。即使 det (A) < 0,R 的行列式也保证保持 =1。
代码如下
1 | |
那么东西都说完,接下来就开始按一开说的大致做
先用 id 把 index 记录下来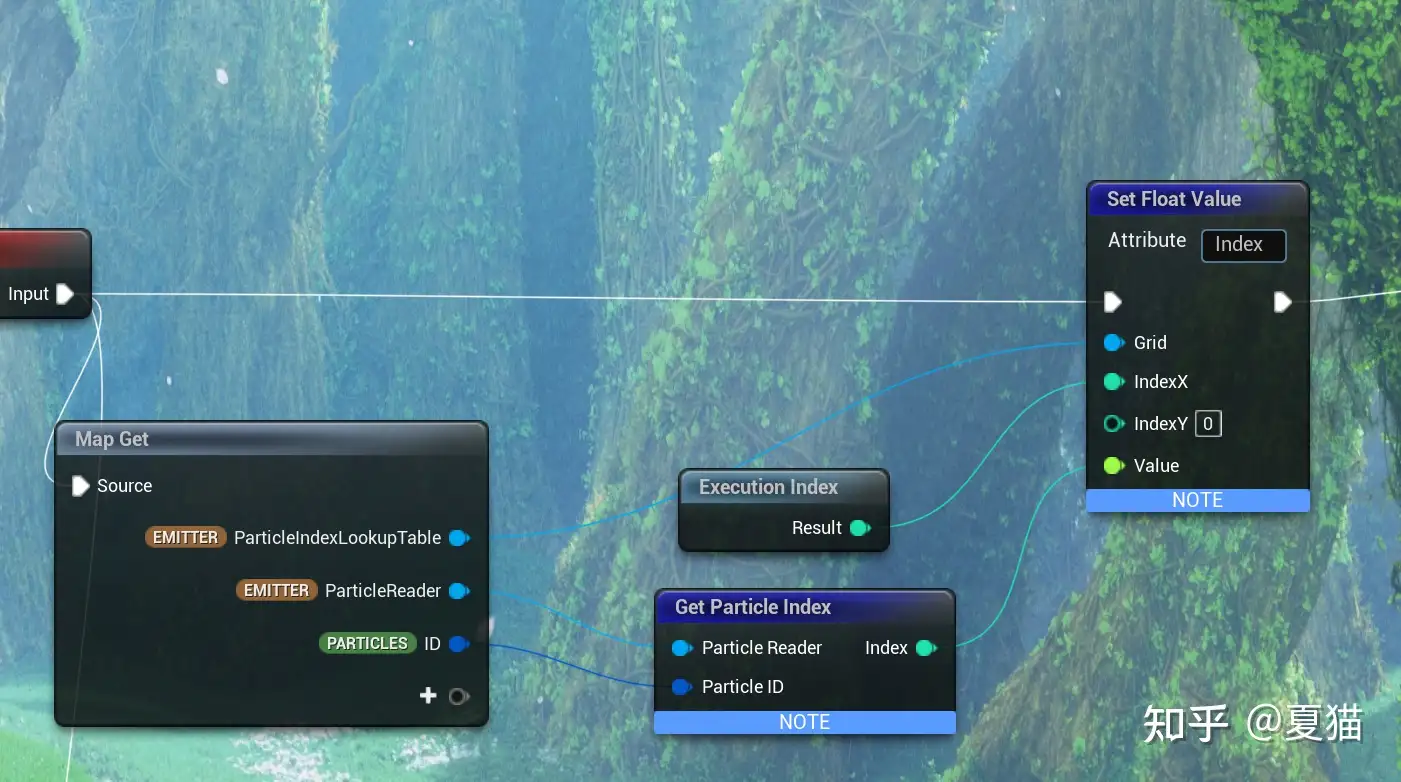
sdf collision 就陷入多深就直接给他多少力拉回来,简单粗暴
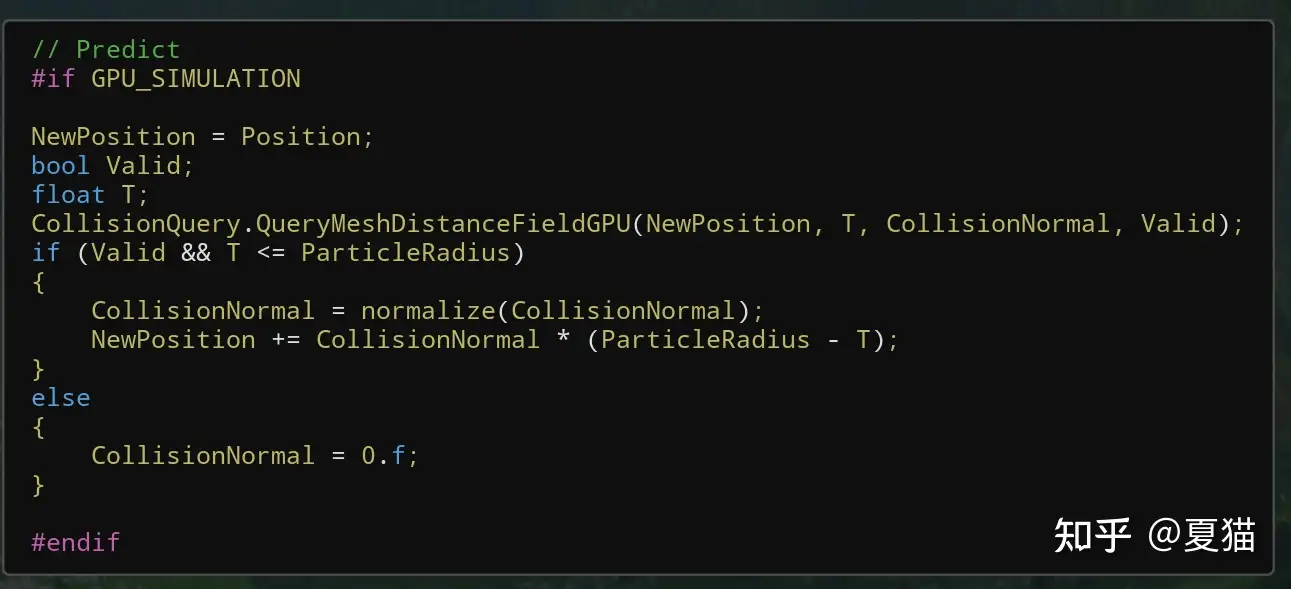
更新 Shape Matching 位置并写入 grid2d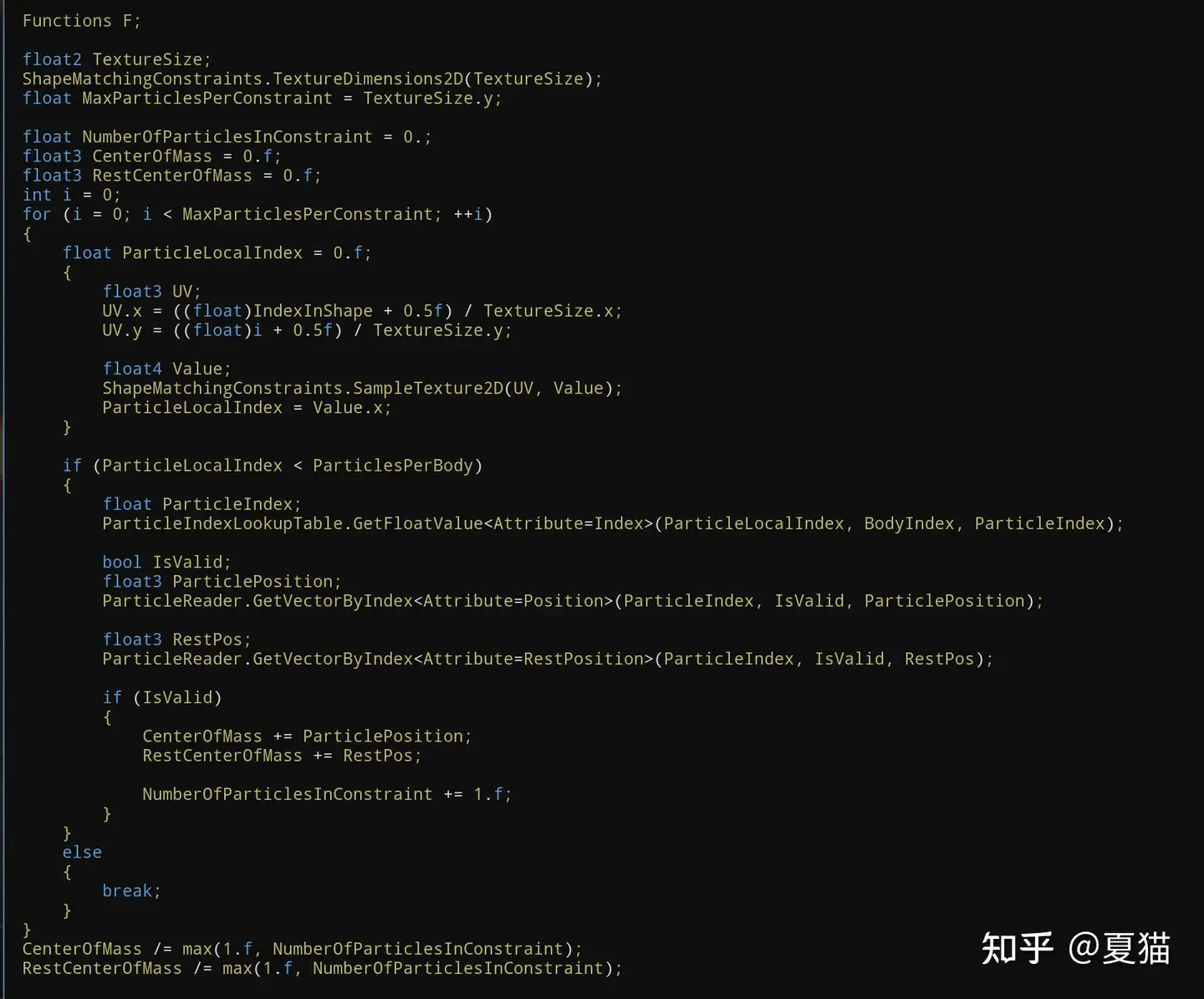

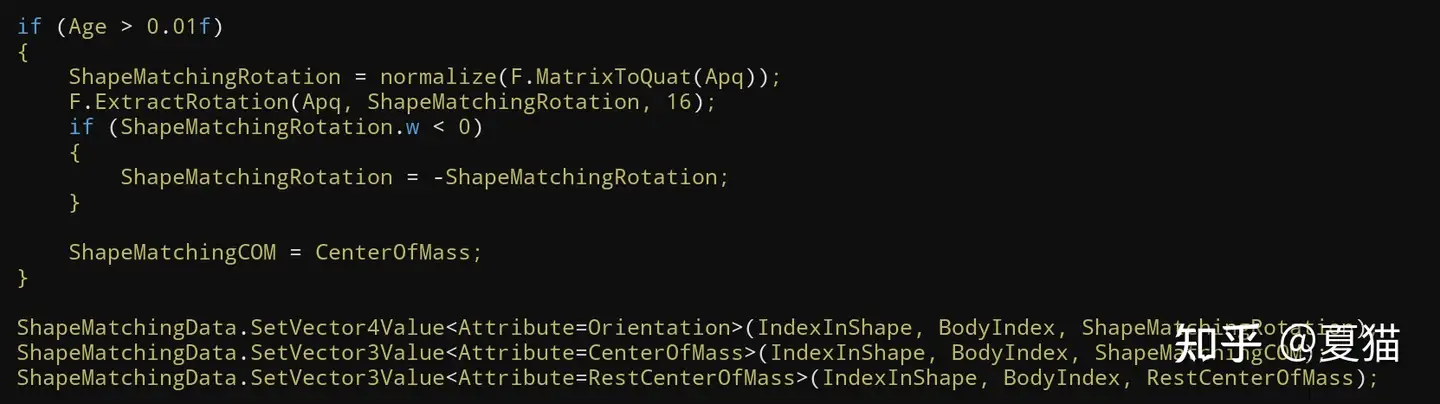
写完 grid2d 下个 simulation stage 直接读取做 lerp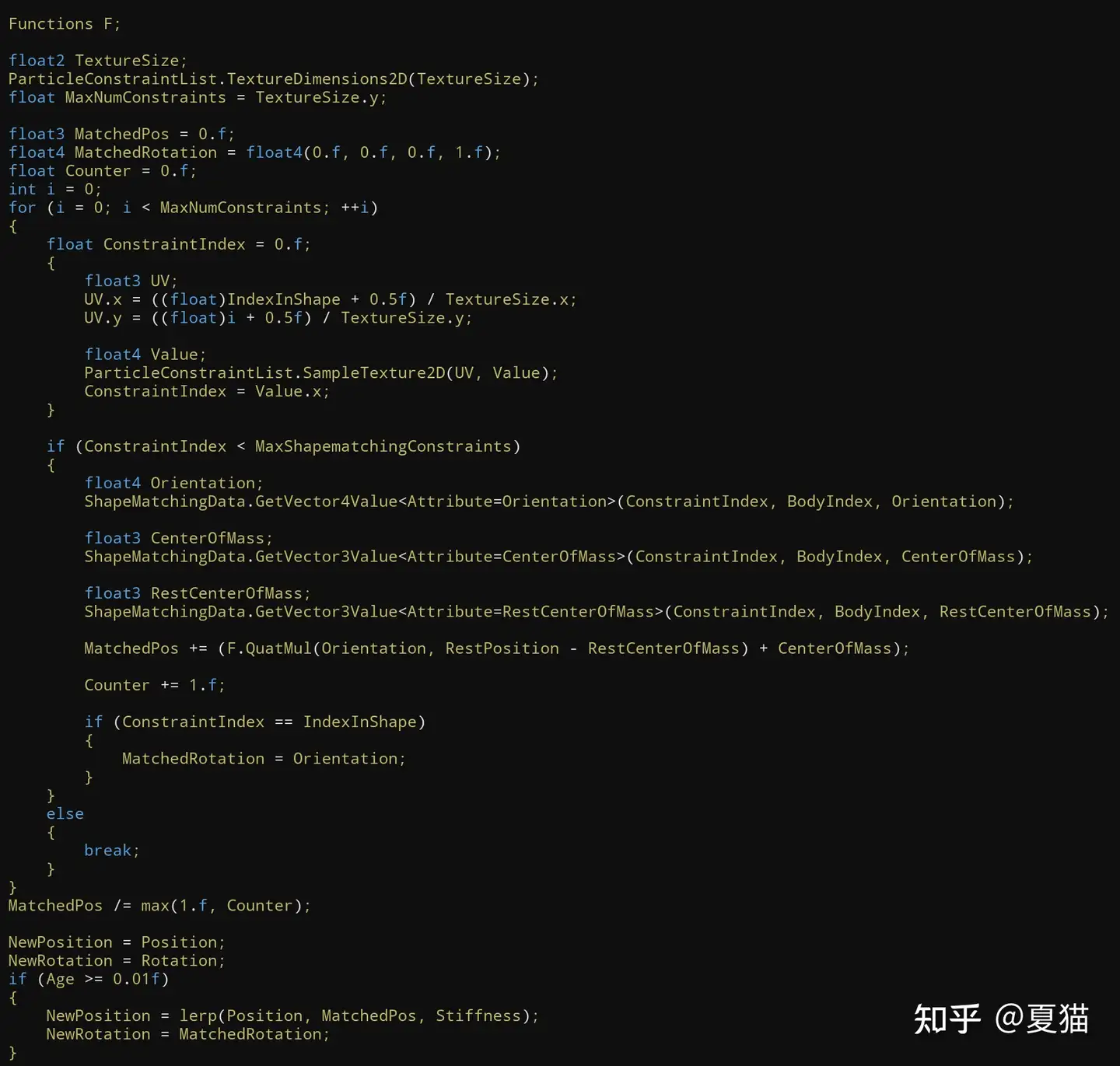
就这样简单的得到了现在 position 和 rotation
顺便说个小技巧,写 function 可以直接写结构体,在结构体里面写,调用这个结构体就行,像材质 custom node 一样,其中文中里面的旋转矩阵和四元数转换或者四元数相乘都可以从官方节点哪里拿来。