首页 文章

# MPM 水

# 简介

对于流体模拟来说有两种视界，一种是拉格朗日视角一种是欧拉视角，

  • 拉格朗日视角就是把物理量存在粒子上，因为粒子是自由移动，所以很容易做 advection，做起动量守恒很容易，但粒子是离散化，使得检测周围邻居变得异常困难，但可以用哈希结构数据储存来检索，就像 niagara neighbor 3d
  • 欧拉视角则是把世界分为一个个 grid，所有物理量在都是在 Grid 上，因为是 Grid 所以很容易求出 Projection，就是压强，但欧拉 grid 面对 advection 很难，模拟的时候回流能量损失，流体看起来非常粘

而 MPM 质点法就是混合了拉格朗日视角和欧拉视角，他由 FLIP 方法的扩展而提出的，FLIP 就是现在官方 Niagara 中所使用的模拟方法。而 MPM 的好处是实现起来很简单，可以模拟各种离散材料，并且可以让他们互相作用，例如水和沙子之间互相作用，或者 softbody 和 water 和雪之间的互相作用，在模拟水这一块，FLIP 用的是隐式积分，要几十次迭代求解压力场才能收敛，而且需要求多个 Grid 求 Δ，MPM 在运行速率比 FLIP 的快一点。

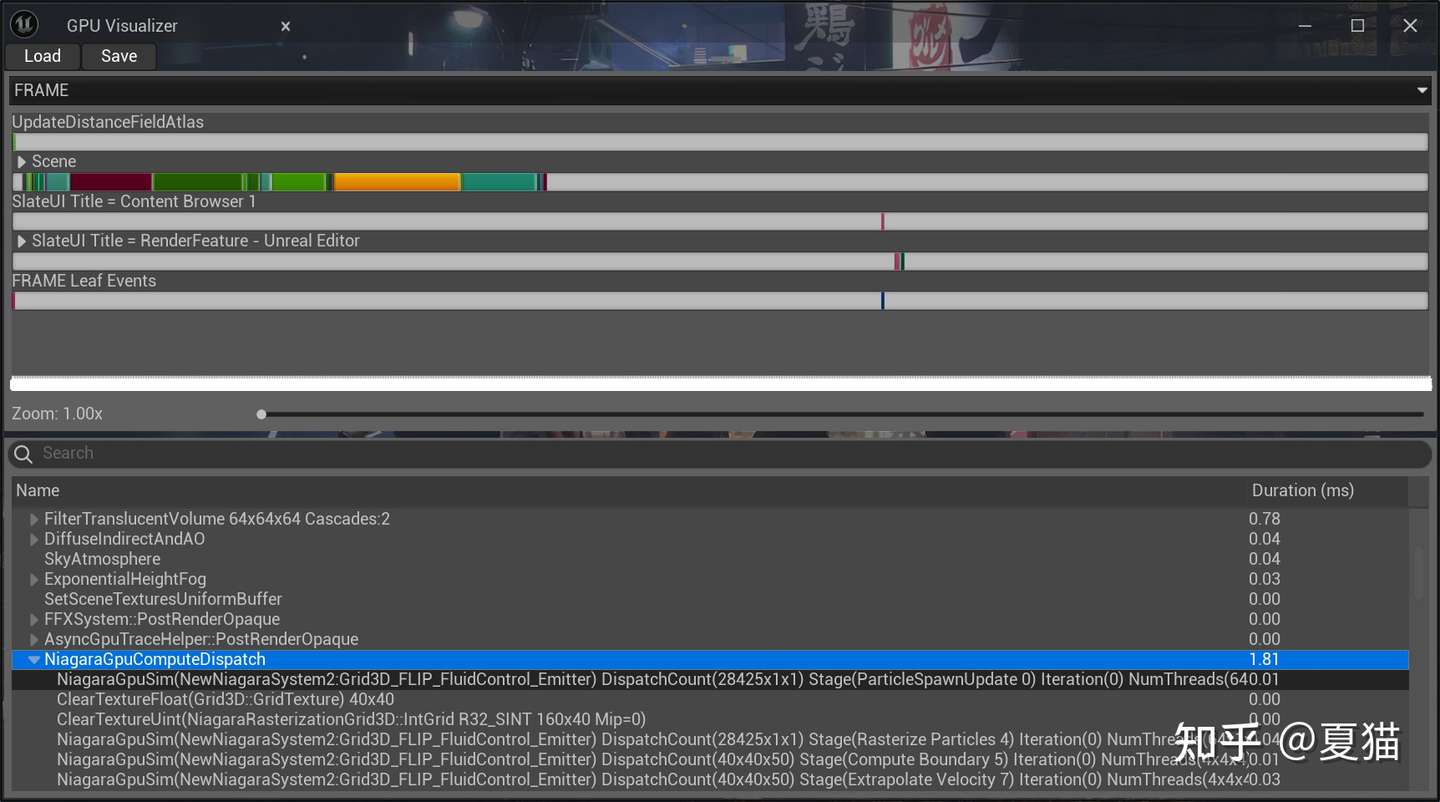
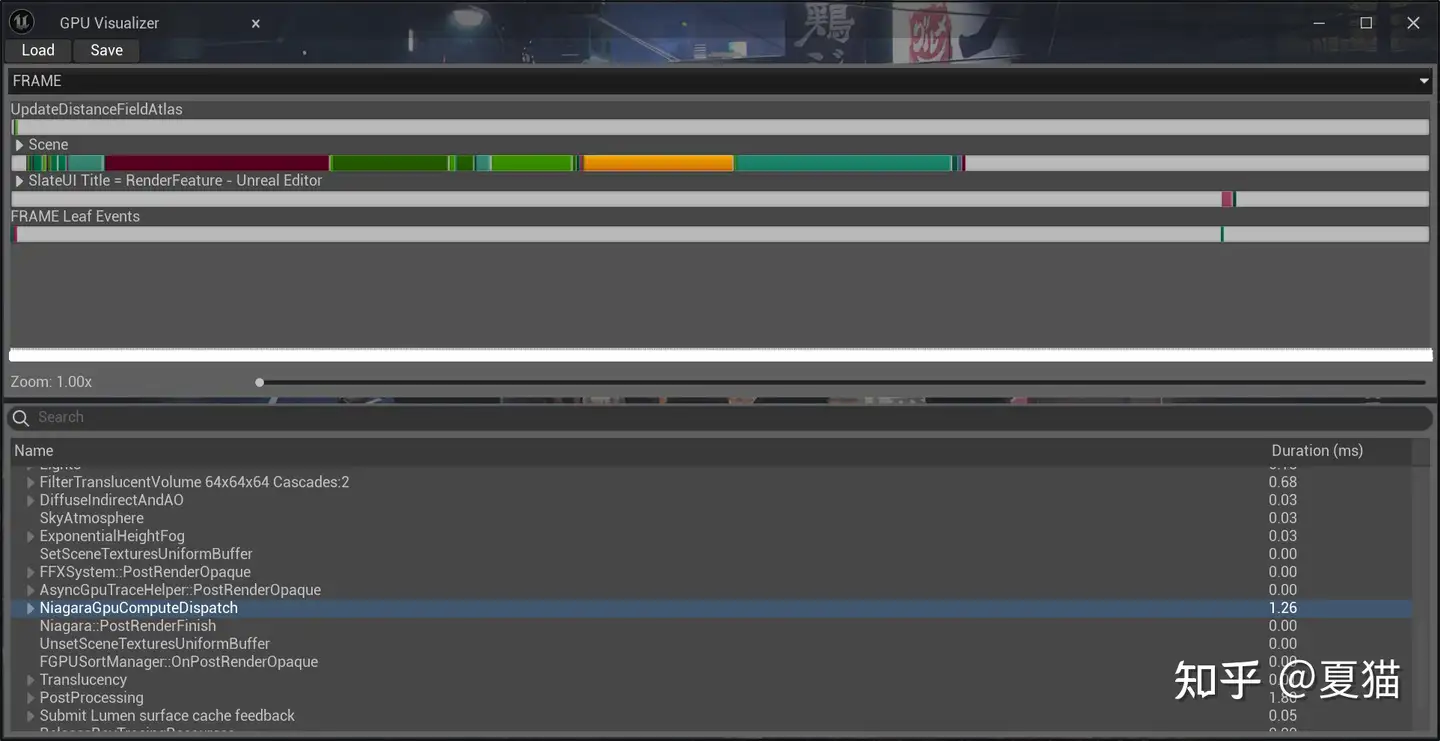
测试两个系统同时运行一秒后，在 50 个格子的精度下，spawn rate 是 20000 情况下，压力场迭代 200 次官方水是 1.81 秒，MLS-MPM 是 1.26 秒

https://pic1.zhimg.com/80/v2-0d309551850d112f81f4051c9750a784_1440w.jpg

官方 FLIP 水

https://pic3.zhimg.com/80/v2-86cfc2dab0b0b5d1272ecb779587c91e_1440w.webp

# MPM

PIC（particle in cell）是在 MPM 框架下最初提出来的 method，MPM simulation 大致实现的步骤就是先把粒子插值分配到周围 Grid 上（particle to grid），然后在 Grid 上计算力和各种互相作用力，然后再插值回粒子求出速度（ grid to particle）

# PIC - Particle In Cell

先把粒子通过 B-Spline 插值到 3x3，一般就是用 Quadratic 足够 smooth

这是代码，看起来简单明了，这个过程就叫 P2G，其中插值不是以当前点为中心，而且粒子点所在的 3x3 区块的右下角，所以 base 才有 - 0.5

然后 Grid 上动量除于 Mass 就是速度了

https://pic1.zhimg.com/80/v2-88f270d40eb60e9cd79b42016bd15fdc_1440w.webp

最后把网格速度重新收集到粒子上，再 B-Spline 插值回去

但是这个 method 有个问题就是有能量损耗，，平移没有耗散，但拉式，旋转，剪切都是有耗散的，运动一会就不动了，原因是信息的丢失，在原来二维的 Grid 上有 18 个自由度，3x3 个格子和各个 xy，但传播到粒子上就只有两个自由度，就是只有 xy。

解决办法就是给粒子记录更多信息，就是 APIC，多了一 C 矩阵，记录 x y 方向的拉伸、剪切旋转量、剪切量

还有个方法就是只传输 Δx 信息，就是对格子求导得到最终速度给粒子，就是 FLIP

# APIC-affine particle in cell

先看看 particle to grid 的公式，

将每个粒子的质量分配到该粒子周围的网格上，并使用粒子的速度及 affine 矩阵计算每个网格的速度。

(mv)in+1=∑pwi,p[mpvpn+mpCpn(xi−xpn)](m\textbf{v} )_i^{n+1}=\sum_pw_{i,p} [m_p \textbf{v}_p^{n}+m_p\textbf{C}_p^n(\textbf{x}_i-\textbf{x}_p^n)]

min+1=∑pmpwi,pm_i^{n+1}=\sum_pm_pw_{i,p}

其中， wi,pw_{i,p} 表示点 pp 对网格 ii 的贡献权重， Cpn\textbf{C}_p^n 表示 affine 矩阵，下标pp 的意思就是粒子，下标ii 就是网格位置，那么 xi\textbf{x}_i 就是 3x3 的 Base 点

对于 APIC 的实现公式很简单，但其推导及其复杂，所以就不写推导了

APIC 在 PIC 上多加了一个矩阵和 affine

v2-7ef74b2a9a1f493de74e36f71a47d2ac_1440w.png

然后 Grid to Particle 公式就是下面，同时为每个粒子计算 affine 矩阵。

vpn+1=∑iwi,pvin+1Cpn+1=4Δx2∑iwi,pvin+1(xi−xpn)Txpn+1=xpn+Δtvpn+1\textbf{v}_p^{n+1}=\sum_iw_{i,p}\textbf{v}_i^{n+1} \\\textbf{C}_p^{n+1}=\frac{4}{\Delta x^2}\sum_iw_{i,p}\textbf{v}_i^{n+1}(\textbf x_i-\textbf x_p^n)^{\textbf T} \\\textbf{x}_p^{n+1}=\textbf{x}_p^n+\Delta t \textbf{v}_p^{n+1} \\

vin+1(xi−xpn)T\textbf{v}_i^{n+1}(\textbf x_i-\textbf x_p^n)^{\textbf T} 就是 V 对 Base Grid 的 outer-product 外积，在这里说一下，国内很多中文文章把 crose 叉积当成外积用，写出去误导了很多人，但百度百科和维基是对的，在线性代数中一般指两个向量的张量积，两个向量外积是个矩阵，是向量 A 乘向量 B 的转置

这是 APIC 论文，有兴趣可以读读

https://www.math.ucla.edu/~cffjiang/research/apic/paper.pdf

# MLS-MPM

那么现在就到本文在 Niagara 实现的方法，就是在 APIC 上进行了改进，在 APIC 上多了个 stress，称为 Cauchy Stress，起到的作用是表现抵抗压缩的力，在 P2G 公式是这样的

Fpn+1=(I+ΔtCpn)Fpn(mv)in=∑pwi,p{mpvpn+[mpCpn−4ΔtΔx2∑pVp0P(Fpn+1)(Fpn+1)T](xi−xpn)}min+1=∑pmpwi,j\textbf{F}_p^{n+1}=(\textbf I+\Delta t \textbf C_p^n)\textbf{F}_p^{n} \\(m\textbf v)_i^{n}=\sum_pw_{i,p} \left\{ m_p \textbf v_p^n+\left[m_p\textbf C_p^n-\frac{4\Delta t}{\Delta x^2}\sum_p V_p^0\textbf P(\textbf F_p^{n+1})(\textbf F_p^{n+1})^T \right](\textbf x_i-\textbf x_p^n)\right\}\\ m_i^{n+1}=\sum_pm_pw_{i,j}\\

其中，Fpn\textbf F_p^n 表示形变梯度，P(Fpn)\textbf P(\textbf F_p^{n}) 表示 PK1 数，MLS-MPM 方法除了处理流体，还会用来解弹性物体，所以不再有投影步骤，所以他和 APIC 的区别只有 P2G 过程。

v2-d423f3cf45c0b0c828bfc1169d416851_1440w.png

# MLS-MPM 公式推导

那么中间那一项是怎么得出来的呢，首先要求出当前点的动量，那么该点所受到一定是冲量叠加上去的，假设我们用超弹性材料模型

v2-f03d5a118ca8ffd4672da68ffbcc45ea_1440w.png

而所受到的的力就是总体弹性势能求导，其中 ψp\psi_p 是粒子受到的弹性势能密度， VpV_p 就是粒子初始体积，2D 就是 Δx 的平方，3D 模拟就是立方，则 U 就是痛的弹性势能，但在 MLS-MPM 他的 Grid 是不会变的，那么需要用另一种方法法。

假设我们 Particle 向前移动 τ\tau ，而 τ\tau 无限接近于 0，而黄色的 X 就是形变 Grid，那么把所有的东西替换成我们的变量，那么当前点所受到的势能就是公式 5。现在因为 MLS-MPM 的 Grid 是不变的，所有转化成对ViV_i 求导，所以需要除于 τ\tau ，然后用链式法则把（6）变成（7）拆成 3 项，而这三项就可以定义，那么现在可以发现红色那一项就是 PK1 stress 了，蓝色项就是事先定于的形变矩阵，绿色对 C 求导就是直接是 APIC 中的 C，做完后，就可以把 τ\tau 消除掉，于是就得到 MLS-MPM 的公式了

v2-229b25e581200e16ef38aa59aeb228f0_1440w.png

这是 MLS-MPM 原论文，由胡渊鸣 大佬写的，也可以看一下 Games201

# Niagara 实现

从上面可以知道 MLS-MPM 是实现起来非常简单，运行性能也很快，所以在 Niagara 实现也很简洁

首先是设置 Grid3d，这里要用到原子操作，所以要用到 Rasterization Grid3D，这里有很奇怪的 bug，在跑 Rasterization Grid3D 一定要带 Grid3D 一起玩，否则粒子动一下就不动了。

v2-22686bbc34c85b103d92c57ed1a8a53f_1440w.png

因为要把速度和质量写入 grid3d，所以 RasGrid 的 NumAttribute 要开 4 个，我写 7 个是因为还要把颜色写入可以做不同发射源做颜色混合。

# initial

v2-0945fa51c723f78144ce20bc43582a6d_1440w.png

# P2G

然后做 P2G 操作，这里我写了个很傻的模组，就是把粒子 trasform 到 Grid 空间，就是把位置和速度归化 0-1，因为我们是显示积分，要是用世界位置的话，一下子数字就 inf 就炸开了，在官方有个 module 可以直接用来算矩阵然后 mul position 就行了

v2-c8ef84a9f1d21e1bd9ba02d56f32e013_1440w.png

v2-97dddfc76a2d55d66244e0e93ce997e4_1440w.png

在流体模拟里面，形变矩阵 F 会随着时间变得越来越大，但模拟到一定时候后，float 这时候精度就不够用了，为了解决问题，在 A.P Tampubolon et al. (2017) 这篇文章中我们可以用 F 的行列式来表示整个矩阵的变化，这时候我们就可以用去记录 F，用 J 来代替，J 的定义如下。其中矩阵 C 对体积有贡献的只有对角线，所以就用 C 的迹

v2-bd21270d3d3e3e27f65946c562093af9_1440w.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
int Cellx;
int Celly;
int Cellz;
RasterizationGrid3D.GetNumCells(Cellx, Celly, Cellz);
float dx = 1/(float)Cellx;
float3 CellPosition = Position * Cellx;
float3 BasePosition = floor(CellPosition - 0.5);
float3 FPosition = CellPosition - BasePosition;
TestVector = FPosition;
float3 Weight[3];
float IGNORE ;
Weight[0] = 0.5 * (1.5 - FPosition) * (1.5 - FPosition);
Weight[1] = 0.75 - (FPosition - 1) * (FPosition - 1);
Weight[2] = 0.5 * (FPosition - 0.5) * (FPosition - 0.5);
float DeltaDx = dx*dx;
float pvol = pow(dx*0.5 ,3);
J = J * (1 + DeltaTime * (C[0][0] + C[1][1] + C[2][2]));
OutJ = J;
float Stress = -DeltaTime * 4.0 * E * pvol * (J - 1) / DeltaDx;
float4x4 Affine = {
Stress,0,0,0,
0,Stress,0,0,
0,0,Stress,0,
0,0,0,0
};
Affine += Mass * C;
for(int x = 0;x<3;x++)
{
    for(int y = 0; y < 3; y++)
    {
        for(int z = 0; z<3; z++)
        {
            float3 offset = float3(x,y,z);
            float3 Dpos = (offset - FPosition) * dx;
            int IndexX = BasePosition.x + offset.x;
            int IndexY = BasePosition.y + offset.y;
            int IndexZ = BasePosition.z + offset.z;
            if(IndexX < Cellx&&IndexY < Celly&&IndexZ < Cellz&&
                IndexX > 0&&IndexY > 0&&IndexZ > 0)
            {
                float CellWeight = Weight[x].x*Weight[y].y*Weight[z].z;
                float4 GridData = 0;
               
                float3 GridVelocity ;//= GridData.xyz ;
                float4 Mpos = float4(Dpos,0);
                GridVelocity = CellWeight*(Mass * Velocity + mul(Mpos,Affine));
               
                float GridMass ;//= GridData.w;
                GridMass =  CellWeight * Mass;
                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 0, GridVelocity.x,IGNORE);
                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 1, GridVelocity.y,IGNORE);
                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 2, GridVelocity.z,IGNORE);
                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 3, GridMass,IGNORE);
                

                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 4,Color.x *CellWeight ,IGNORE);
                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 5, Color.y *CellWeight,IGNORE);
                RasterizationGrid3D.InterlockedAddFloatGridValue(IndexX, IndexY, IndexZ, 6, Color.z *CellWeight,IGNORE);
                //Grid3D.SetVector4ValueAtIndex(IndexX, IndexY, IndexZ, 0, float4(GridVelocity,GridMass));

            }
            

        }
    }
}

# G2P

因为我没有做什么其他物质之间的交互，所以我们省略中间对 Grid 的操作，还有一点就是我不知道为什么单独操作 Rasterization Grid3D, 值是 0，所以我放弃这一个，直接合到 G2P 过程，并且在这里做 Bound 操作

v2-496faff3e90cfa377765ed7d354768ff_1440w.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
int Cellx;
int Celly;
int Cellz;
RasterizationGrid3D.GetNumCells(Cellx, Celly, Cellz);
float dx = 1/(float)Cellx; //(float)Cellx / WorldSize.x;
float3 CellPosition =Position*Cellx;
float3 BasePosition = floor(CellPosition - 0.5);
float3 FPosition = CellPosition - BasePosition;
float3 Weight[3];

Weight[0] = 0.5 * (1.5 - FPosition) * (1.5 - FPosition);
Weight[1] = 0.75 - (FPosition - 1) * (FPosition - 1);
Weight[2] = 0.5 * (FPosition - 0.5) * (FPosition - 0.5);
float DeltaDx = dx * dx;
NewV = 0;
float4x4 C = 0;
Test = dx;
OutColor = 0;
for(int x = 0;x<3;x++)
{
    for(int y = 0; y < 3; y++)
    {
        for(int z = 0; z<3; z++)
        {
            float3 offset = float3(x,y,z);
            float3 Dpos = (offset - FPosition) * dx;
            
            int IndexX = BasePosition.x + offset.x;
            int IndexY = BasePosition.y + offset.y;
            int IndexZ = BasePosition.z + offset.z;
            if(IndexX < Cellx&&IndexY < Celly&&IndexZ < Cellz&&
                IndexX > 0&&IndexY > 0&&IndexZ > 0)
            {
                float CellWeight = Weight[x].x*Weight[y].y*Weight[z].z;
                float4 GridData;
                
                //Grid3DCollection.GetPreviousVector4ValueAtIndex(IndexX, IndexY, IndexZ, 0, GridData);
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 0, GridData.x);
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 1, GridData.y);
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 2, GridData.z);
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 3, GridData.w);
                float3 TempColor = 0;
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 4, TempColor.x);
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 5, TempColor.y);
                RasterizationGrid3D.GetFloatGridValue(IndexX, IndexY, IndexZ, 6, TempColor.z);
                OutColor +=TempColor.xyz * CellWeight*BlendColor;

				if(GridData.w > 0)
				{
				    GridData.xyz /= GridData.w;
				}
				GridData.xyz -= DeltaTime * G;
				 float DistanceToNearestSurface;
				float3 FieldGradient;
				 bool IsDistanceFieldValid;
				CollisionQuery.QueryMeshDistanceFieldGPU(float3(IndexX,IndexY,IndexZ)*(WorldSize/Cellx),  DistanceToNearestSurface,  FieldGradient, IsDistanceFieldValid);

				if(IndexX > Cellx - Bound && GridData.x > 0)
				{
				    GridData.x *=-Elasticity;
				}
				if(IndexX < Bound && GridData.x < 0)
				{
				    GridData.x *=-Elasticity;
				}
				if(IndexY > Celly - Bound && GridData.y > 0)
				{
				    GridData.y *=-Elasticity;
				}
				if(IndexY <  Bound && GridData.y < 0)
				{
				    GridData.y *=-Elasticity;
				}
				if(IndexZ > Cellz - Bound && GridData.z > 0)
				{
				    GridData.z *=0;
				}
				if(IndexZ <  Bound && GridData.z < 0)
				{
				    GridData.z*=0;
				}
				if(IsDistanceFieldValid&&DistanceToNearestSurface <3)
				{
				    //float3 CollisionVelocity =(normalize( GridData.xyz )+normalize(FieldGradient))*length(GridData.xyz)*0.9 ;
				    GridData.xyz =lerp(normalize( GridData.xyz ),normalize(FieldGradient),1)*length(GridData.xyz)*1.5;
				}
                float3 GridVelocity = GridData.xyz  ;
                NewV += CellWeight * GridVelocity;
                //Dpos = normalize(Dpos);
                float4x4 GOuterProduct = {
                GridVelocity.x * Dpos.x, GridVelocity.x * Dpos.y, GridVelocity.x * Dpos.z,0,
                GridVelocity.y * Dpos.x, GridVelocity.y * Dpos.y, GridVelocity.y * Dpos.z,0,
                GridVelocity.z * Dpos.x, GridVelocity.z * Dpos.y, GridVelocity.z * Dpos.z,0,
                0,0,0,0
                };                //NewC=  GOuterProduct ;
                C += 4 * CellWeight * GOuterProduct / DeltaDx;
            }
            
        }
    }
}
OutColor = saturate(lerp(Color,OutColor,0.01));
float colF1 = length(C[0]);
float colF2 = length(C[1]);
float colF3 = length(C[2]);
float Fa = length(float3(colF1,colF2,colF3));
if(Fa >50)
{
   C /=2.f;
   /*for(int i = 0;i<4;i++)
    {
        for(int j = 0 ;j < 4; j++)
        {
            C[i][j] = clamp(C[i][j],-10,10);
        }
    }*/
}
//NewV.z -= 98.f;
NewC = C ;

更新于

请我喝[茶]~(￣▽￣)~*

Natsuneko 微信支付

微信支付

Natsuneko 支付宝

支付宝

Natsuneko 贝宝

贝宝